排料问题

ZhuYuanxiang 2023-02-14 11:47:31
Categories： Tags：

排样问题

排样问题，也称为下料问题，排料问题，是一个在工业生产中有关广泛应用的重要问题。主要来源于服装制造、钢铁切割、家具制造等制造工业中的零件下料，研究目标在于如何充分使用原材料，减少消耗，提高效益。数学描述：如何将形状放置进入固定尺寸的窗口中，在保证没有重叠的情况，使得容器最小或者容器内空间利用率最高。

排样问题的广泛应用的启发式算法就是左底排样算法，形状是逐一加入，放置的时候尽量从左底部开始，这个方案可以获得初始解。基于此算法，有两个主流分支：第一，基于序列检索，即修改加入序列从而获得更优解；第二，基于布局检索，即在获得初始解之后，直接对形状的位置进行修改，从而获得更优解。同时，最新的研究中，也有通过直接几何法将其转化为整数规划问题、对边界非直线情况的解决方案，允许自由旋转的解决方案等

重要术语

中文术语

不规则排样问题（Irregular Packing
Problems）：将一系列不规则图形放置在某一面板上，使得某个目标函数值最优化。

二维决策问题（Decision
Problem，DP）：给定一组不规则图形和一块面板，判断其是否能够将所有图形均放置在给定面板中

二维背包问题（Knapsack
Problem，KP）：给定一组不规则图形和一块面板，找出不规则图形的一个子集放置在面板上，使得面板的利用率最大化

二维装箱问题（Bin-packing
Problem，BP）：给定一组不规则图形和一组面板，将所有图形放置在给定面板上，使得面板的使用量最小

二维带状填充问题（Strip-packing
Problem，SP）：给定一组不规则图形和一块宽度固定、长度不限的矩形面板，将所有图形放置在给定面板上，使得矩形被占用的长度最小。

英文术语

irregular packing

nesting

irregular shape stock cutting

strip packing

irregular-shape cutting

packing of polygons

研究现状

排样问题属于NPC问题，即无法在多项式时间内获得最优解。因此排样算法一方面研究如何提高多边形间几何计算正确性，并且降低其计算复杂度；另一方面研究将智能算法应用于排样算法之中。

排样问题中常用的启发式算法是左底部排样算法，基于这个算法的两个主流方向：

  1. 基于序列检索，即修改形状加入的序列以获得最优解
  2. 基于布局检索，即在获得初始解之后，直接对形状的位置进行修改，从而获得更优解

Art等人提出临界多边形（NFP）来解决二维图形之间的靠接问题，Burke等人针对NFP提出了包含弧线的NFP计算方法。NFP能够快速对两个任意形状的多边形进行重叠判断，完整保留不规则件的形状信息进行排样，而不需要拟合成规则件后进行排样。

排样问题中确定零件的排放次序和零件的定位规则是重点和难点。对于零件的定位规则，最早由Art提出的“左侧靠接”定位规则

规则矩形排样问题

已经日趋完善[^1]。

[^1]: Wei LJ, Zhang Df, Chen QS, A least wasted first heuristic algorithm for the rectangular packing problem, Computers and Operations Research, 2009, 36(5):1608-1614

不规则矩形排样问题

不规则图形需要满足的约束：

  1. 任意两个图形不能相互重叠

  2. 所有图形必须完全包含在面板内部

二维不规则排样问题的分类：

  1. 二维决策问题

  2. 二维背包问题

  3. 二维装箱问题

  4. 二维带状填充问题

二维不规则排样问题的难点：

  1. 组合难度：在所有零件均为矩形时，问题也是 NP 难的

  2. 几何难度：二维不规则排样问题所涉及的几何运算主要在于判断给定的两个不规则图形是否重叠。

    1. 更多的几何计算时间。

    2. 问题搜索空间提高，几何复杂度的提高对算法的效果产生了质的影响

      1. 矩形排样问题，本质上其潜在的可行放置的分布是离散的

      2. 不规则排样问题，可行放置的分布是连续的，需要在算法中压缩问题的解空间

    3. 更多的旋转角

      1. 矩形排样问题，受矩形的对称性和正交性影响，只需要考虑一种旋转——直角旋转，即只考虑矩形水平旋转和竖直旋转两种情形

      2. 不规则排样问题，理论上需要考虑任意角度的旋转，导致解空间无限增长

基本几何问题

不规则图形通常采用多边形近似，因此在给定两个多边形 P 和 Q 的定义及其信息位置时，应用计算机排样时需要解决的基本几何问题：

  1. 多边形 P 和 Q 是否重叠？

  2. 如果 P 和 Q 重叠，如何分离？

  3. 对于随机算法，如果重叠，试描述重叠的程度

几何问题处理方法

对于基本的几何问题，经典的处理方法：简单多边形包裹法，位图法（Raster
method）、临界多边形（No-fit polygon，NFP）法。

如果给定多边形为凸多边形时，则可以使用一个更加简洁的算法。[^2]

[^2]: Bennell JA, Oliveira JF. The geometry of nesting problems: A tutorial, European Journal of Operational Research, 2008, 184(2):397-415

简单多边形包裹法

将不规则的图形使用简单的规则多边形（通常为矩形）包裹，把复杂图形位置关系的判定转化成包裹后的简单图形位置关系的判定。

缺点：由于没有充分利用所给的几何信息，经常造成较多的浪费，于是采用某种迭代压缩策略进行改进。[^3],
[^4]

[^3]: Jakobs S. On genetic algorithms for the packing of polygons, European Journal of Operational Research, 1996, 88: 165-181

[^4]: Heckmann R, Lengauer T. A simulated annealing approach to the nesting problem in the textile manufacturing industry, Annals of Operations Research, 1995, 57: 103-133

位图法

将连续的区域划分成离散的网格近似表示，然后对这些离散网格编码，从而将连续的几何信息变换为用矩阵表示的离散信息。

优点：算法简单，实现容易

缺点：离散化粒度会影响解的质量

不同的编码方式产生了不同的表示方法。

临界多边形法

首次引入[^5]，主要思想：通过构造两个多边形的临界多边形，将判定两个多边形的位置关系问题转化成判定点和多边形的位置关系问题。

[^5]: Albano A, Sappupo G. Optimal allocation of two-dimensional irregular shapes using heuristic search methods, IEEE Transactions on SYstems, Man and Cybernetics, 1980, 5:242-248

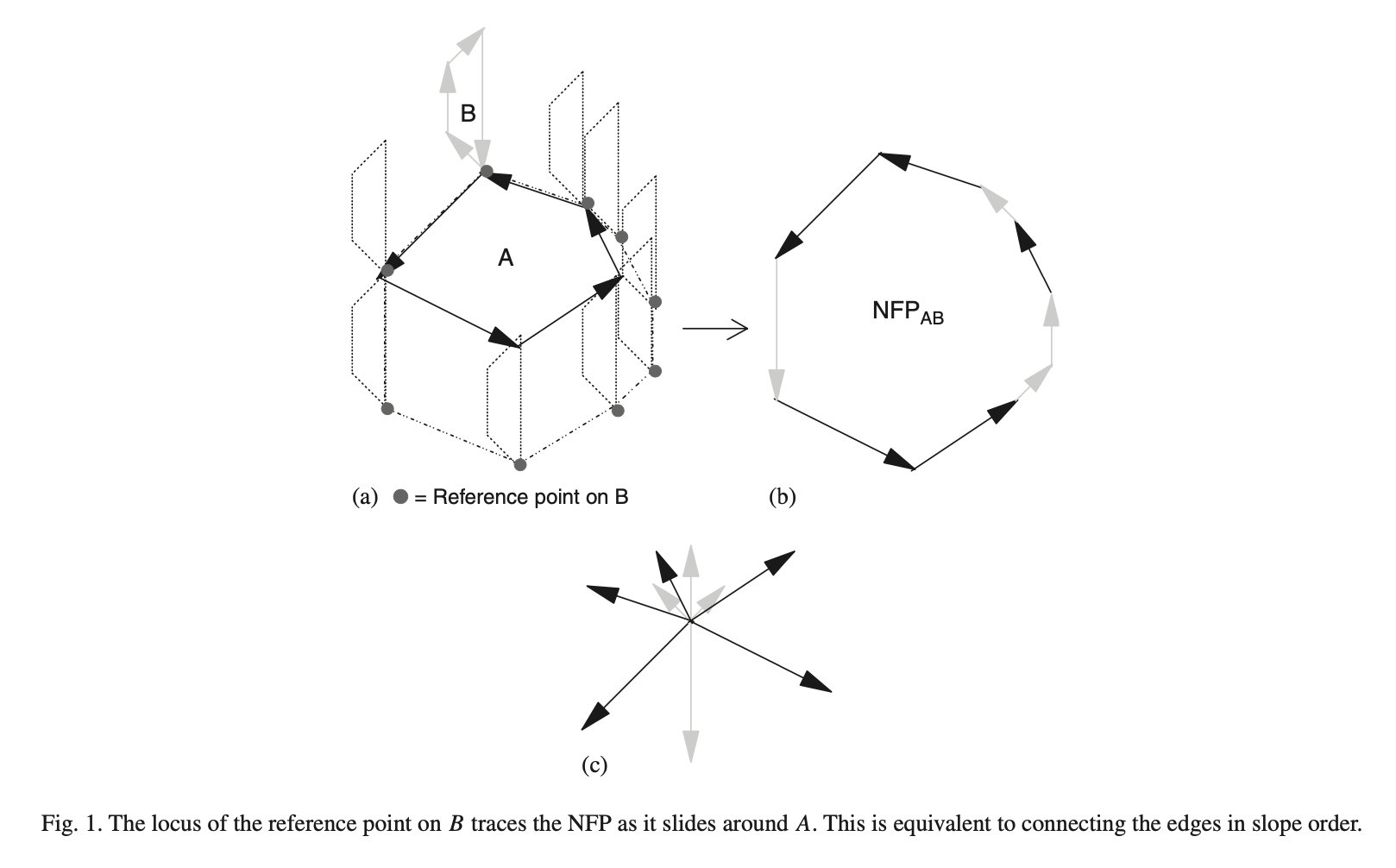
image-20200317165731944

优点：与前面的近似处理不同，临界多边形法直接使用原多边形，因此得到的结果更加精确，效率也更高。并且临界多边形的构造可以离线完成，从而完成构造后，最终排料问题的时间复杂度为
$$O(n)$$​ 缺点：临界多边形的构造算法相对复杂，实现困难。

现有的多边形构造算法分类：

  1. 滑动算法（Sliding Algorithm）[^6]：

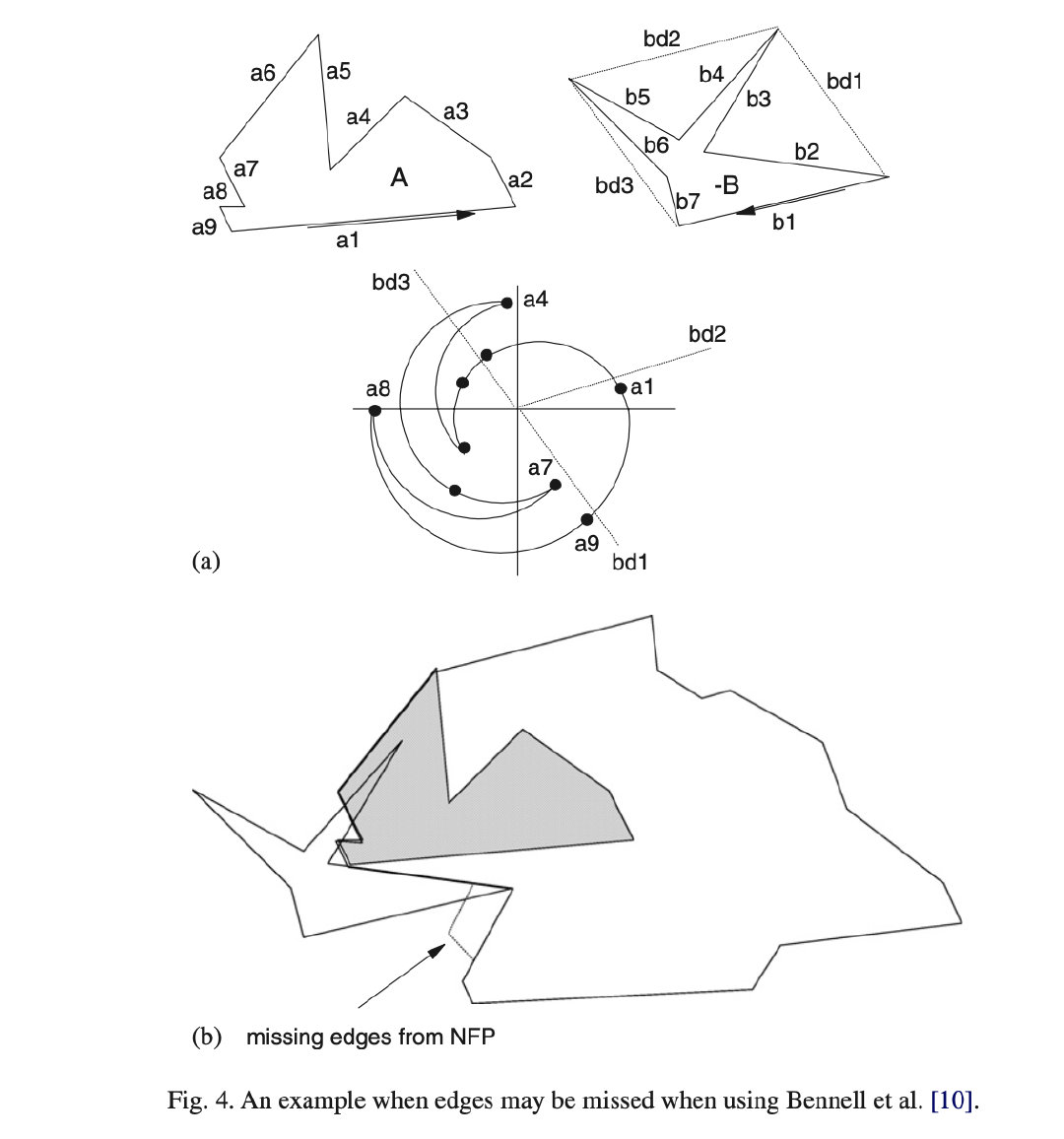
  2. 基于 Minkowski 和的构造算法[^7],[^8]：image-20200317165803931

  3. 基于多边形剖分的构造算法[^9],[^10]：

[^6]: Burke EK, Hellier RSR, Kendall G, Whitwell G. Complete and robust no-fit polygon generation for the irregular stock cutting problem, Eruopean Journal of Operational Research, 2007, 179:27-49

[^7]: Benell JA, Song X. A comprehensive and robust procedure for obtaining the nofit polygon using Minkowski sums, Computers & Operations Research, 2008, 35(1):267-281

[^8]: Benell JA, Dowsland KA, Dowsland WB. The irregular cutting-stock problem, a new procedure for deriving the no-fit polygon, Computers & Operations Research, 2001, 28:271-287

[^9]: Agarwal PK, Flato E, Halperin, D. Polygon decomposition for efficient construction of Minkowski sums, Computational Geometry Theory and Applications, 2002, 21:29-61

[^10]: Li Z, Milenkovic V. Compaction and separation algorithms for non-convex polygons and their application, European Journal of Operations Research, 1995, 84:539-561

旋转方法

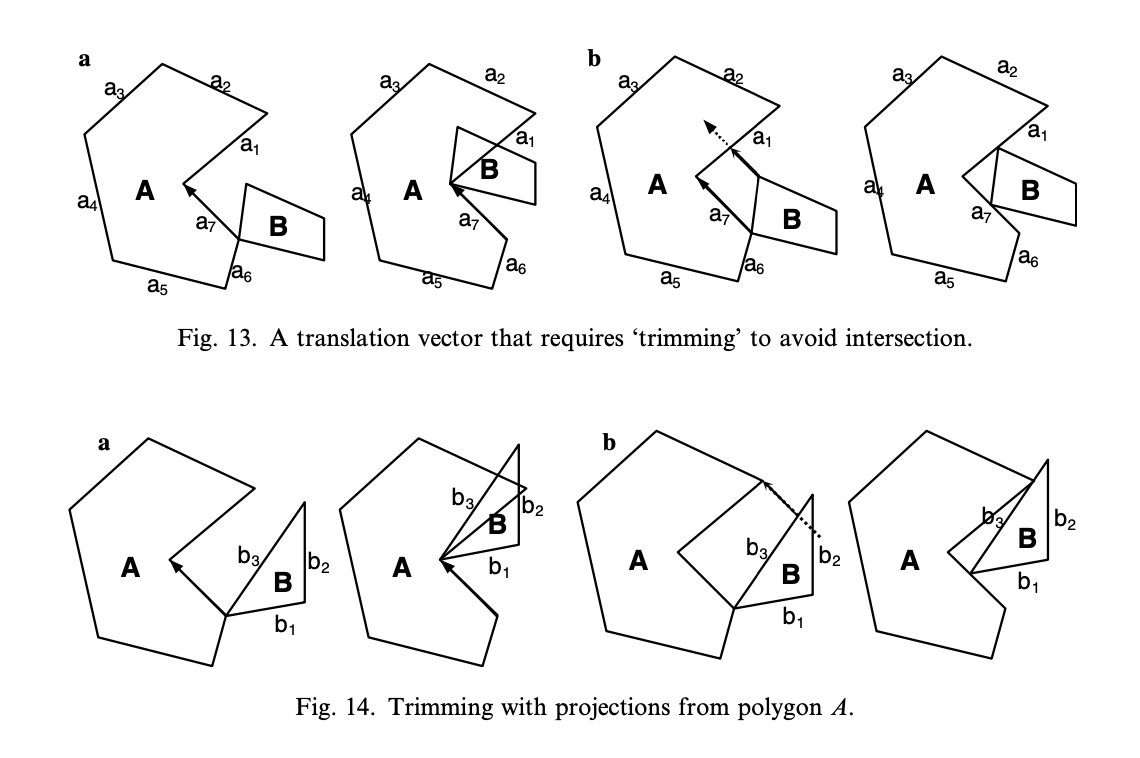
image-20200317165851784

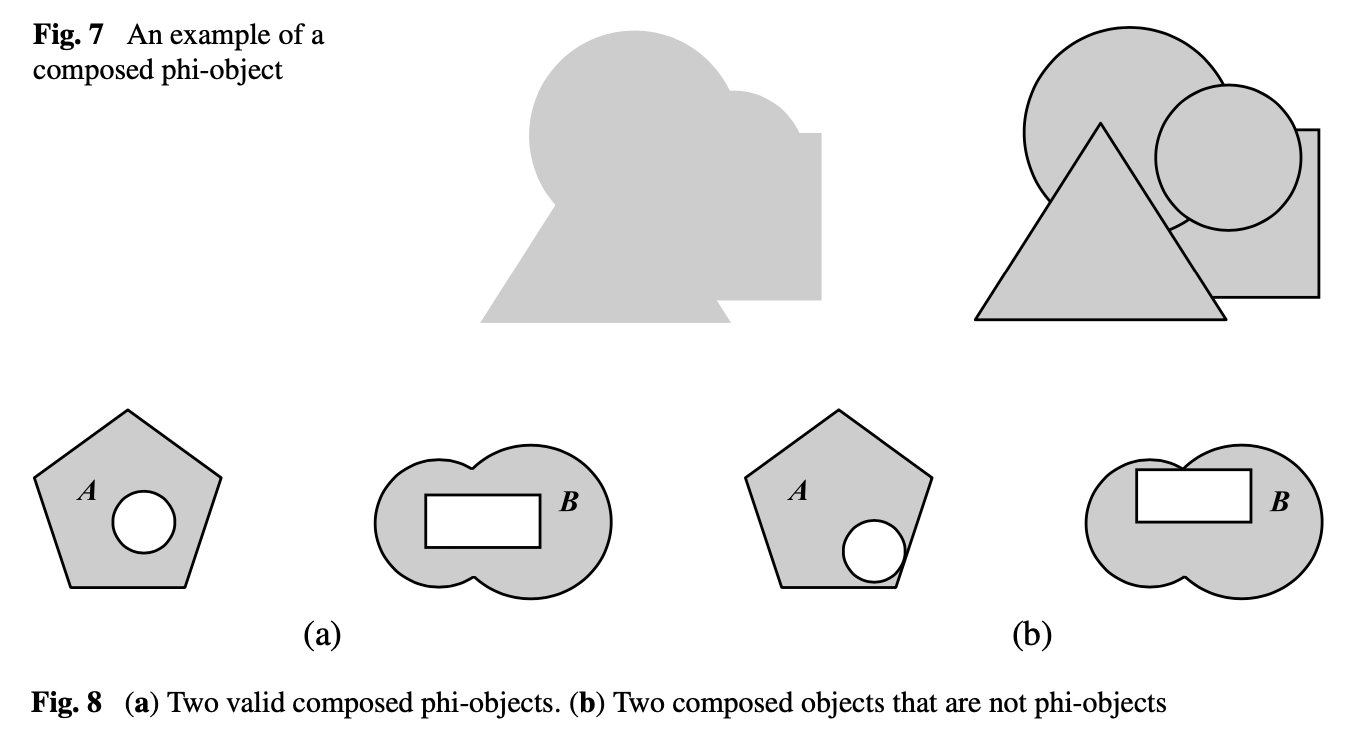
Phi-Function

image-20200317170009933

基于序列检索

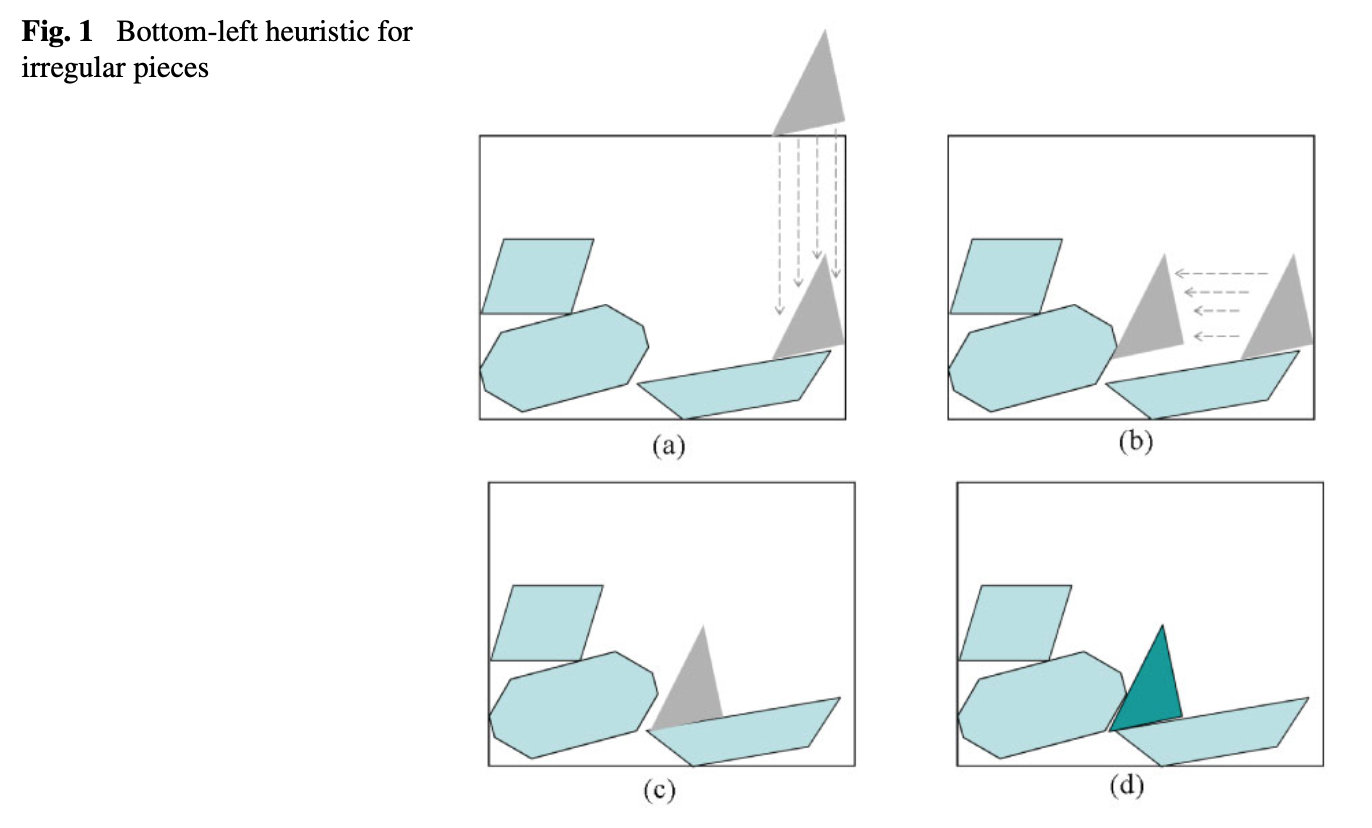
左底部排样

image-20200317165654869

优化算法

遗传算法

模拟退火算法

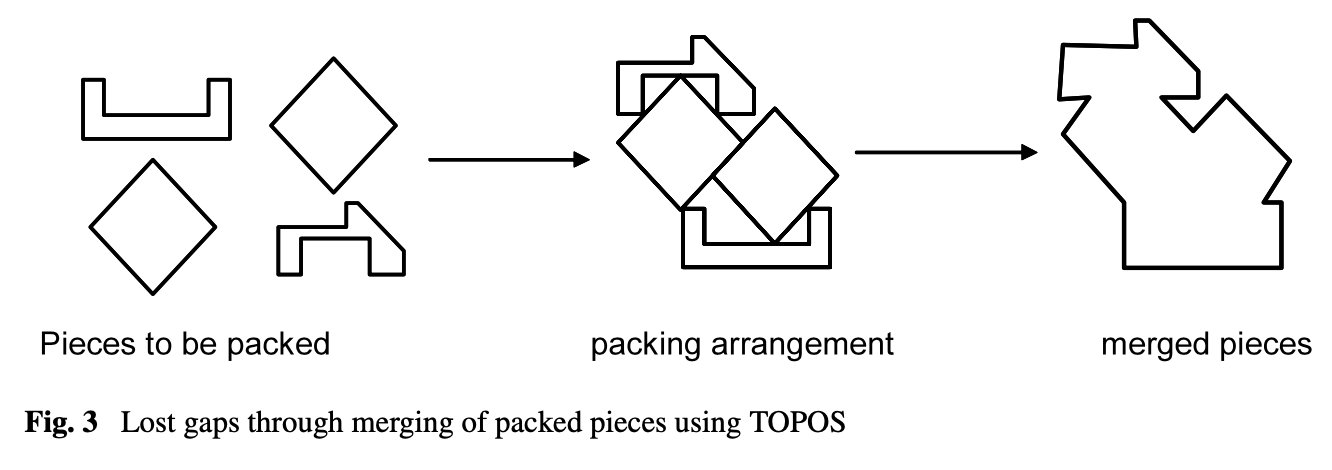
TOPOS

普通方法

image-20200317165617575

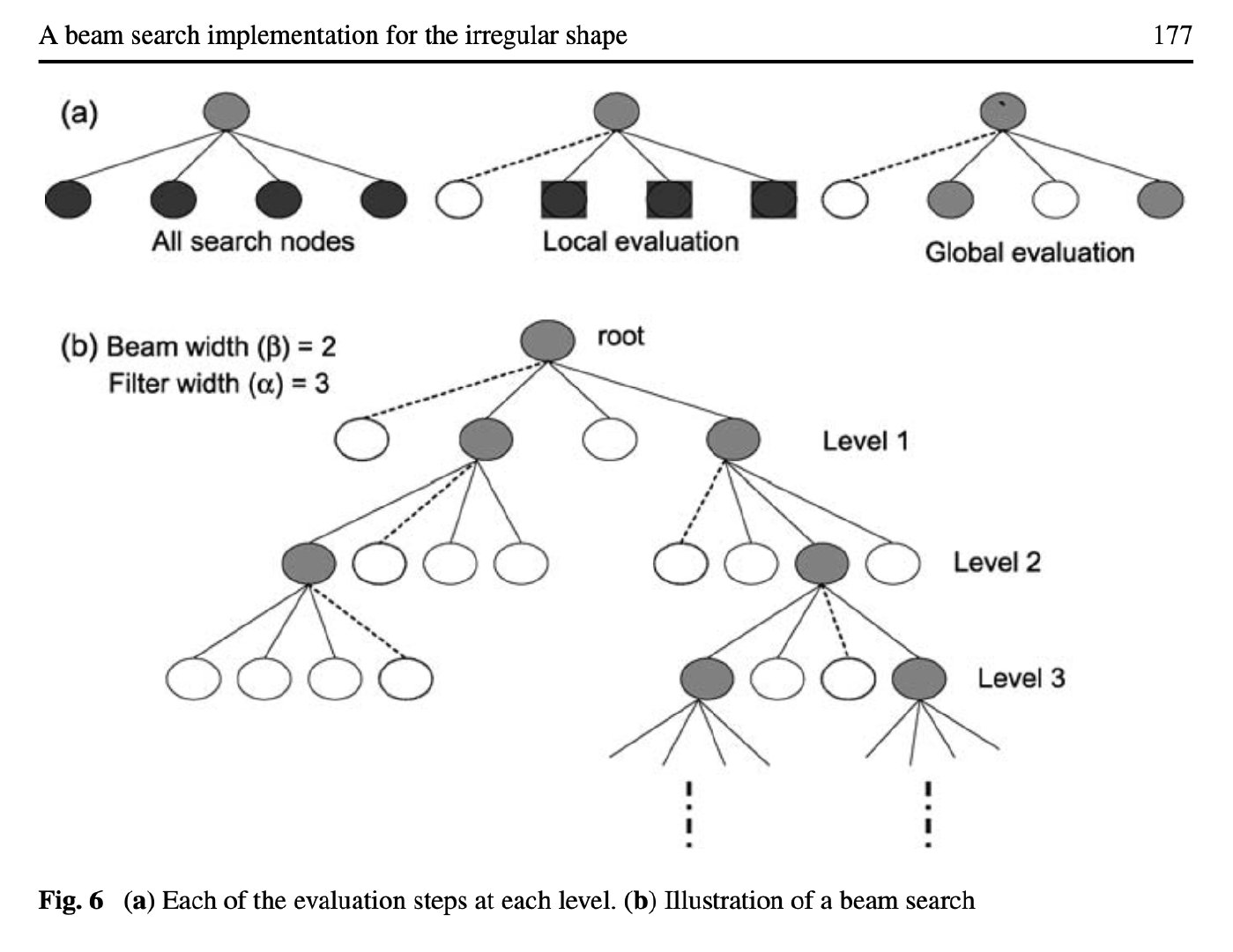
image-20200317165443794

局部优化算法

压缩（Compaction）

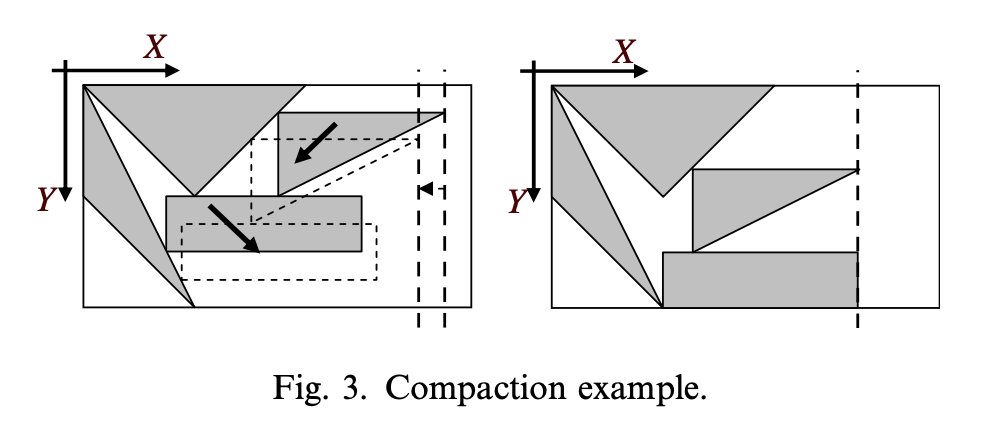
image-20200317165247871

拆分（Separation）

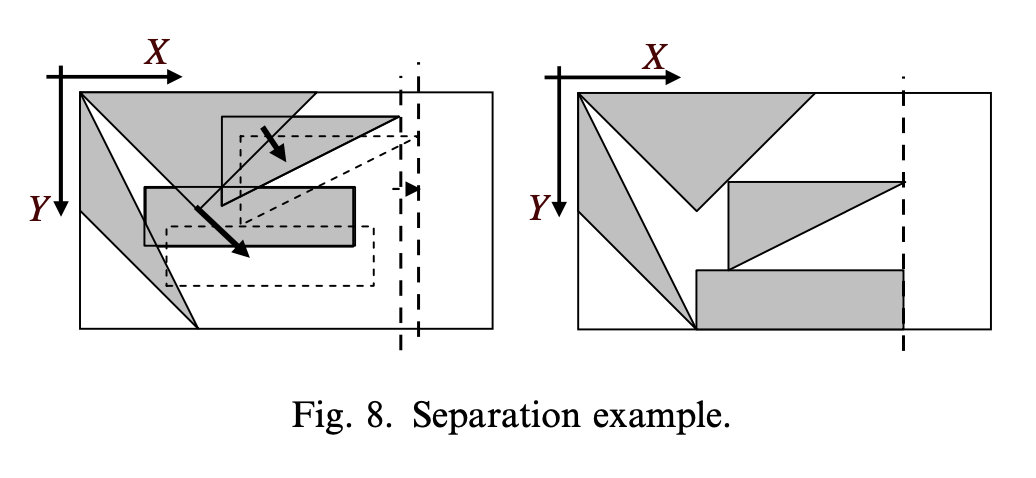
image-20200317165313522

基于布局搜索

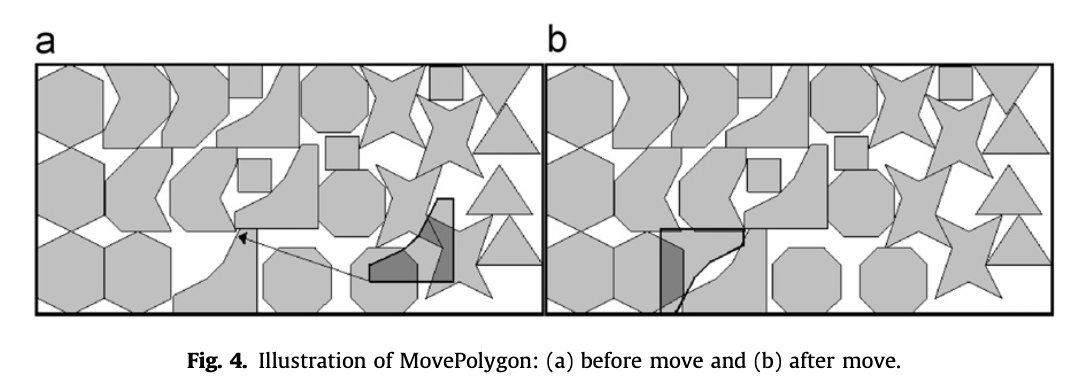
基于布谷鸟检索（Cuckoo Search）的排样算法：是2009年提出的一种自然启发的随机优化算法，可以对解空间进行比较完整的检索，从而最优解，优化了选择检测的局部性问题，在较多数据集中获得最优解的算法，也是对限制旋转角度的数据集研究最多的算法。

基本操作：压缩边界后，将有重叠的开关按照重叠面积或者其他原则，逐步移到 IFR 重叠最小或者没有重叠的地方，直到布局可行，从而实现优化。由于 IFR 的可行域是无法全部枚举的，所以论文主要通过切割检索范围、利用合适的检索方法，找到最合适的新位置。

快速局部检索

Egeblad在2007年第一次提出：在一个共有$$n$$条边的形状组合的区域中，寻找一个$$m$$条边的形状，将寻找最小重叠面积的时间压缩到$$O(mn\log(mn))$$，将平移导致的形状间的重叠区域的变化转化为平移导致的边与边的位置关系的变化；同时采用引导式局部检索，用参数调整后的重叠面积作为选择参考，避免因为某个形状无法找到更优位置，导致陷入局部最优。

核心思路：压缩边界后，选择重叠最大（参数调整后）的形状，进行水平或者垂直移动寻找重叠最小或者没有重叠的位置（检索算法），或者旋转，重复这个步骤直到消除重叠后再次压缩边界。

边界收缩（Shrink）算法在论文寻找。[^11]

[^11]: Egeblad J, Nielsen B K, Odgaard A. Fast neighborhood search for two-and
three-dimensional nesting problems, European Journal of Operational
Research, 2007, 183(3):1249-1266

局部检索迭代

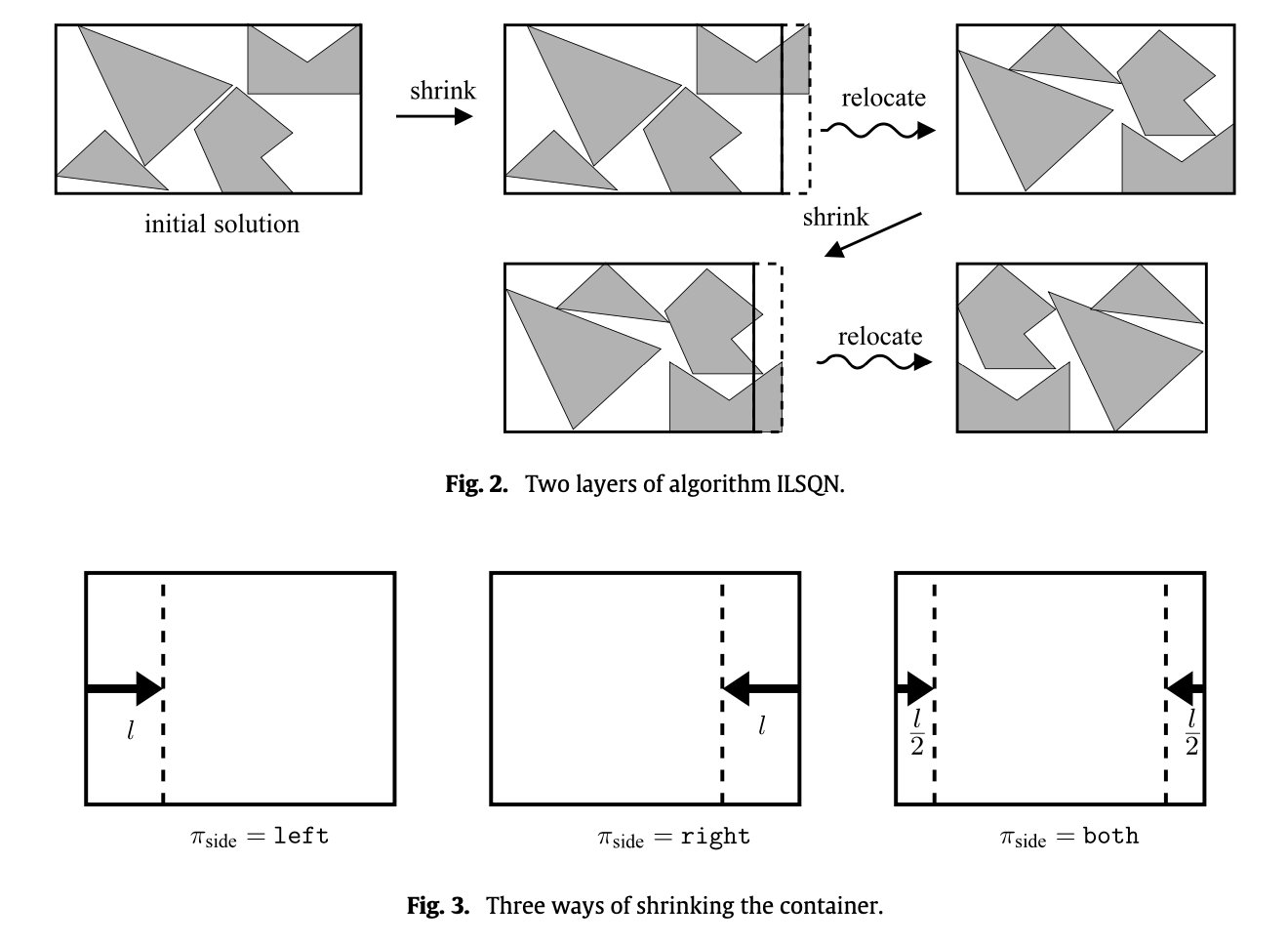
image-20200317170117014

局部检索延长

image-20200317170214433

局部检索引导

参考文献

Spatial Transformer Networks