PCN：点补全网络

ZhuYuanxiang 2021-11-18 00:00:00
Categories： Tags：

PCN：点补全网络

PCN Point Completion Network.pdf

Yuan W, Khot T, Held D, et al. Pcn: Point completion network[C]//2018 International Conference on 3D Vision (3DV). IEEE, 2018: 728-737.

作者的原始实现

PCN 的其他实现

摘要

形状补全，是许多视觉和机器人应用的核心问题。目标是从部分观测中估计对象的完整几何形状。在本文中，我们提出了点补全网络（Point Completion Network, PCN），一种新颖的基于学习的形状补全方法。与现有的形状补全方法不同，PCN直接对原始点云进行操作，没有任何关于底层形状的结构假设（如：对称性）或者标注（如：语义类别）。它的特点是一个解码器的设计，能够生成细粒度的补全，同时维护少量的参数。我们的实验表明，PCN在基于不同水平的不完整数据和噪声的输入（包括来自KITTI数据集中使用激光雷达扫描得到的汽车数据）下都在现实结构的缺失区域中补全了稠密的、完整的点云。代码、数据和训练模型参见PCN Tensorflow 实现。

Ch01 介绍

现实的3D数据经常是不完整的、存在几何和语义信息的损失。例如：由于数据点的稀疏性和有限的传感器的分辨率和遮挡，图1中激光雷达扫描的汽车很难被识别。在本文中，我们展示了一种使用编码器–解码器网络的、新颖的、基于学习的方法去补全这些局部数据。网络直接映射局部形状到完整形状，两种形状都采用3D点云来表示。

最近许多工作[^9][^48]利用包含合成形状的大数据集去训练深度神经网络，该网络可以从单个视图或者局部视图的组合中推断出完整的几何形状。我们的工作也是受这些工作的启发，但是我们的方法与现有方法的关键区别是三维数据的表示。大多数现有方法将三维数据体素化为占用网格或者距离场，并用卷积网络进行处理。然而，3D体素按照立方速度增长的内存消耗限制了这些方法的输出分辨率。此外，精细的几何信息经常因为离散化而丢失。相比之下，我们是基于原始点云设计网络。这个设计避免了高内存消耗和体素化带来的几何信息损失，并且允许网络生成更加细粒度的补全。

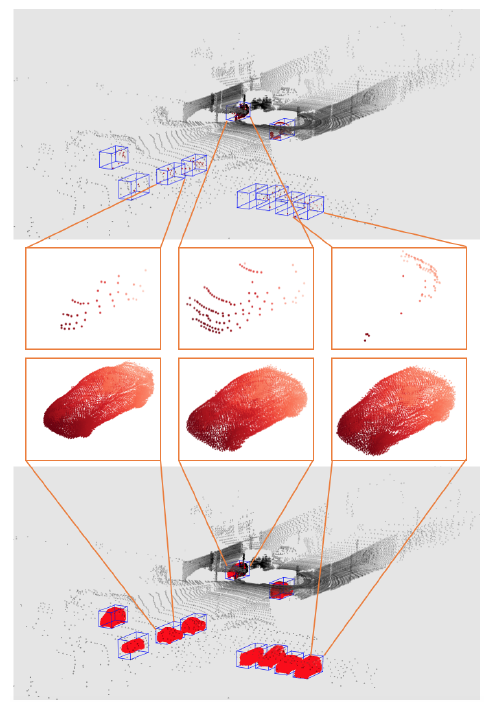
image-20211220164653628

图1：（顶）来自KITTI[^13]的原始激光雷达扫描数据。注意到数据的不完整性使得汽车很少能够被识别。（底）基于PCN生成的完整扫描。从场景中分割出来的独立的汽车点云。

设计一个可以使用和生成点云的网络存在以下几个挑战：

  1. 点云是无序集，这意味着点的排列不会改变它们所代表的几何形状。这就需要设计满足排列不变性的特征提取器和损失函数。
  2. 在点云中没有明确的局部领域的定义，这使得应用任何卷积操作都很困难。
  3. 现有的点云生成网络仅能生成一小部分点，这不足以充分地捕获输出形状的细节。

我们提出的模型解决了这些挑战，而且在单个网络中组合一个排列不变的、非卷积的特征提取器和一个从粗到细的点集生成器，并且对它进行了端到端的训练。

本文的主要贡献：

Ch02 相关工作

3D形状补全

实现3D形状补全的方法大致分为三种：基于几何、基于对齐和基于学习：

点云上的深度学习

我们的研究是基于最近几个对点云进行操作的深度神经网络的最新进展之上。PointNet及其扩展[^37][^38]是这一领域的先驱，也是开展这项工作时的SOTA。它结合了逐点多层感知机与对称聚合函数，获得了排列的不变性和扰动的稳健性，这对于点云的有效特征学习至关重要。从那以后，几种可替代的方法[^23][^51][^53][^57][^58]也被提出。其中有一些方法作为编码器被集成到我们的模型中。

在解码器网络研究上，从学习到的特征生成点集的工作相对较少。[^1]使用全连接解码器，[^11]提出了一种组合全连接层和去卷积层的多分支解码器。最近，[^60]引入了一种有趣的解码器设计，它模拟了2D平面到3D表面的变形。然而，这些方法生成的结果都少于2048个点。我们的模型结合了这些设计的优点，并且以更加高效的方式生成了更高分辨率的输出。

Ch03 问题陈述

设$X$是位于观测对象表面上的一组三维点，这些点是通过单次观测或者三维传感器的一系列观测获得的。设$Y$是从对象的观测到的表面和未观测到的表面随机均匀抽样得到的三维点的稠密集合。我们定义形状补全问题为在给定$X$下预测$Y$。请注意，在这个构想下，$X$不一定是$Y$的子集，并且$X$中的点和$Y$中的点没有明确的对应关系。因为它们都是从潜在的对象表面独立抽样得来的。

我们使用有监督学习来解决这个问题。利用很容易获取$X$和$Y$的样本的大规模合成数据集，我们训练神经网络直接从$X$去预测$Y$。网络在多个对象类别中是通用的，并且对潜在的对象结构没有做任何假设，如：对称性或者平面性。网格架构在Sec04中描述，训练过程在Sec0501中描述。

Ch04 点补全网络

本节描述了我们提出的模型的架构，点补全网络（Point Completion Network，PCN）。如图2所示，PCN是一个编码器–解码器网络。编码器的输入是点云$X$，输出是$k$维特征向量。解码器的输入是$k$维特征向量，输出一个粗略的（course）点云$Y_{course}$和一个精细的（detail）点云$Y_{detail}$。损失函数$L$是计算基准点云$Y_{gt}$和编码器输出之间的差别，然后通过反向传播训练整个网络。请注意，与自动编码器不同，我们没有强制网络在输出中保留输入中的点。相反，网络从局部观测的空间到完整形状的空间中学习了一种投影。接下来，我们描述了编码器、解码器和损失函数的特定设计。

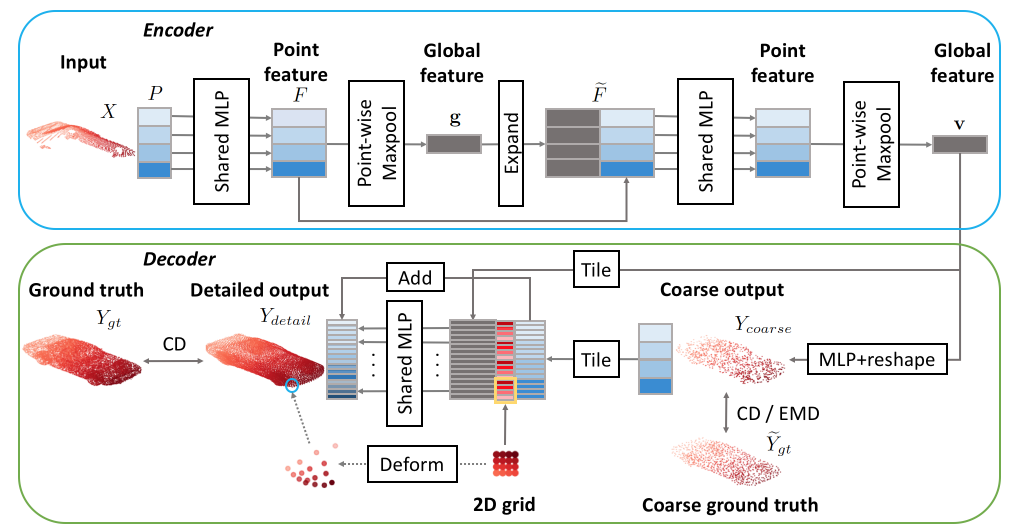
image-20211221172141515

图2：PCN架构。编码器抽象了输入点云$X$为特征向量$\mathbf{v}$。解码器使用$\mathbf{v}$，首先，生成粗略的输出$Y_{coarse}$，然后，生成精细的输出$Y_{detail}$。每个颜色化的方框表示一个矩阵行。相同的颜色指示相同的内容。

4.1. 点特征编码

编码器负责将输入点云中的几何信息总结为特征向量$\mathbf{v}\in\mathbb{R}^k, k=1024$。我们提出的编码器是PointNet的扩展版本，它从PointNet中继承了排列的不变性和对噪声的容忍度，可以处理不同数目的输入点。

具体来说，编码器由两个堆叠的PointNet层组成。

4.2. 多步骤生成点云

解码器负责从特征向量$\mathbf{v}$生成输出的点云。我们提出的解码器在多步骤生成点云的流程中组合了基于全连接的解码器[^1]和基于折叠的解码器[^60]的优点。实验展示了我们的解码器的性能优于基于全连接的解码器或者基于折叠的解码器。

我们主要的观测结果是基于全连接的解码器擅长预测表示形状的全局几何性质的稀疏的点集合。同时，基于折叠的解码器擅长逼近表示形状的局部几何性质的平滑的表面。因此，我们将输出点云的生成分成两个阶段：

我们的网络，在这个多阶段过程中，生成了一个稠密的输出点云，相比全连接解码器使用的参数更少（参见表1），相比基于折叠的解码器灵活性更强。

4.3. 损失函数

损失函数测量输出点云和基准点云之间的差异。因为两个点云都是无序的，损失函数需要对点的排列保持不变。两个候选的排列不变函数由[^11]引入：倒角距离（Chamfer Distance，CD）和地动距离（Earth Mover’s Distance，EMD）^注1
$$
\begin{equation}
CD(S_1,S_2)=
\frac1{|S_1|}\sum_{x\in S_1}\min_{y\in S_2}|x-y|2
+\frac1{|S_2|}\sum{y\in S_2}\min_{x\in S_1}|y-x|2
\end{equation}
$$
等式(1)中的$CD$计算了输入点云$S_1$和基准点云$S_2$之间的平均最近点距离。我们使用的是对称版本的倒角距离，其中第一项强制输出点逼近基准点，第二项保证输出点云覆盖基准点云。请注意，计算$CD$时不需要$S_1$和$S_2$是相同的大小。
$$
\begin{equation}
EMD(S_1,S_2)=\min{\phi:S_1\to S_2}\frac1{|S_1|}\sum_{x\in S_1}|x-\phi(x)|2
\end{equation}
$$
等式(2)中的$EMD$找到一个双射$\phi:S_1\to S_2$，用于最小化对应点之间的平均距离。在实践中，找到最优$\phi$的成本过高，因此我们使用迭代$(1+\epsilon)$的逼近模式[^4]。与$CD$不同，$EMD$需要$S_1$和$S_2$是相同的大小。
$$
\begin{equation}
L(Y{coarse},Y_{detail},Y_{gt})=d_1(Y_{coarse},\tilde{Y}{gt})+\alpha d_2(Y{detail},Y_{gt})
\end{equation}
$$
等式(3)中是我们提出的损失函数，包括两个项$d_1$和$d_2$，超参数$\alpha$控制权重。第一项是粗略输出与基准抽样的子样本$\tilde{Y}{gt}$之间的距离，$\tilde{Y}{gt}$与$Y_{coarse}$大小相同。第二项是精细输出$Y_{detail}$与完整基准$Y_{gt}$之间的距离。

在我们的实验中，我们同时使用$CD$和$EMD$作为$d_1$，仅使用$CD$作为$d_2$。这是因为$EMD$逼近模式的计算复杂度为$O(n^2)$，当$n$比较大时训练期间的计算成本也比较高，而$CD$使用有效的数据结构（如：KDTree）完成最近邻搜索时其计算复杂度为$O(n\log n)$。

附注

Ch05 实验

首先，在本节中描述了如何创建一个大尺度、多类别数据集用于训练我们的模型。其次，通过比较我们的方法与现在的方法形成对比，以及我们的方法在合成形状上的消融版本。最后，展示了真实世界点云的补全结果，并且介绍了这个结果如何帮助下游的任务（如：点云配准，Point Cloud Registration）。

5.1. 数据生成与模型训练

为了训练我们的模型，我们使用来自ShapeNet的合成CAD模型去创建一个大尺度数据集，数据集中包含了成对的局部和完整的点云$(X,Y)$。具体就是，从8个类别（飞机、储藏柜、汽车、椅子、电灯、沙发、桌子、器皿）中选择30974个模型。完整点云是从网格表面均匀抽样16384个点创建的，部分点云是将2.5D深度图反向投影到3D生成的。我们使用反向投影深度图生成部分点云输入，而不是完整点云的子集，是为了将输入分布更加接近真实世界的传感器数据。对于每个模型，8个部分点云来自8个随机分布的视角生成。请注意，部分点云可以拥有不同的尺寸。

我们选择使用合成数据集来生成训练数据，是因为它包含了真实数据集中没有的完整的、精细的对象三维模型。尽管最近出现的数据集（如：ScanNet[^8]和S3DIS[^2]）拥有非常高质量的三维重建，但是这些重建受限于扫描仪的视角而存在缺失区域，因此它们不足以成为我们的模型的基准数据。

我们保留了100个模型用于验证，150个模型用于检测，剩余的模型用于训练。我们的模型都使用初始学习率为0.0001的Adam[^20]优化器进行了50轮训练，批处理大小是32。学习率每5万次衰减$0.7$。

5.2. ShapeNet的补全结果

在本小节中，我们在ShapeNet的合成点云上对比了我们的方法和几个强基线，包括：表示体素网格、我们模型的修改版本。我们还检测了在新颖的形状上我们的方法的泛化能力，以及我们的模型在面对遮挡和噪声时的稳健性。

基线

先前基于点的补全方法，或者假设了输入的点云比我们已经拥有更加完整[^18]，或者使用了形状的先验知识（如：语义分类、对称性、部件分割[^52]），因此无法与我们的方法直接比较。这里，我们对比了我们的模型与四个强基线模型，这类模型与我们的模型一样工作在多类别的对象上，也存在不同程度的不完整性。

  1. 3D-EPN[^9]：这是一类体素补全方法的代表，也是在大型合成数据集上实现了端到端的训练。为了比较3D-EPN的距离场输出与PCN的点云输出，我们将距离场转换为点云，转换方法是在一个很小的值$d$上提取等位面，并且在结果网格上均匀采样16384个点。为了保证比较的公平，我们还转换PCN的点云输出为距离场，转换方法是从网格中心到输出中的最近点计算距离。
  2. FC：这是一个与PCN使用了相同编码器的网络，但是其解码器是一个3层全连接网络，这个网络直接输出16384个点的坐标。
  3. Folding（折叠）：这是一个与PCN使用了相同编码器的网络，但是其解码器纯粹是基于折叠的[^60]，用于将一个$128\times128$的2D栅格转换为3D点云。
  4. PN2：这是一个与PCN使用了相同解码器的网络，但是其编码器是PointNet++[^38]。

我们提供了两种版本的模型用于比较，它们分别是：PCN-CD和PCN-EMD。粗略输出的点的个数$s=1024$，精细输出的点的个数$n=16384$。对于粗略输出的损失函数，PCN-CD使用CD，PCN-EMD使用EMD。请注意，对于精细输出的损失函数，受到EMD的计算复杂度的限制，两种模型都使用CD。

测试集

我们创建了两个测试集：一个是从参与了训练的8个类别中保留的150个形状组成；一个是从没有参与训练的8个类别中保留的150个形状组成。我们将新的类别分成两组：一组在视觉上与训练类别相似：床、长凳、书架和公共汽车；另一组在视觉上与训练类别不相似：吉他、摩托车、手枪和滑板。图3中给出了定理比较结果，图9中给出了定性比较结果。

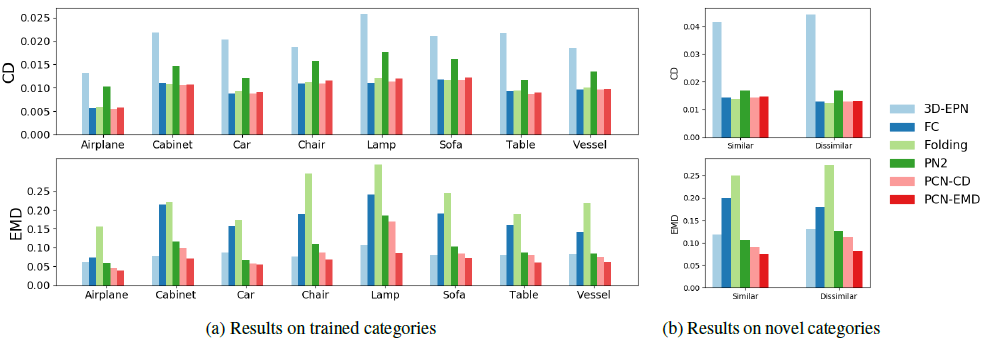
image-20211222135132728

图3：ShapeNet上的定量比较。对于CD（上）和EMD（下），下面的效果更好。(a)展示了从参与了训练的相同类别中测试案例的结果。(b)展示了没有参与训练的类别中测试案例的结果，这些类别分为相似的（公共汽车、床、书架、长凳）和不相似的（吉他、摩托车、滑板、手枪）。

image-20211222141143455

图9：ShapeNet上定性补全结果。上面四行是训练期间使用过的类别的结果。下面四行是训练期间没有见过的类别的结果。

度量

我们在点云上使用的度量是输出的点云和基准点云之间的CD和EMD，定义见Sec0403。图5中使用插图展示了两个度量之间的差别。我们可以看出当全局结构不同时（如：椅子靠背的角附近）CD的值很高。另一方面，EMD更加分散，因为它惩罚了两个点云之间的稠密差。请注意，EMD的均值远大于CD。这是因为EMD需要点之间一对一的对应关系，而CD可以是一对多的对应关系。

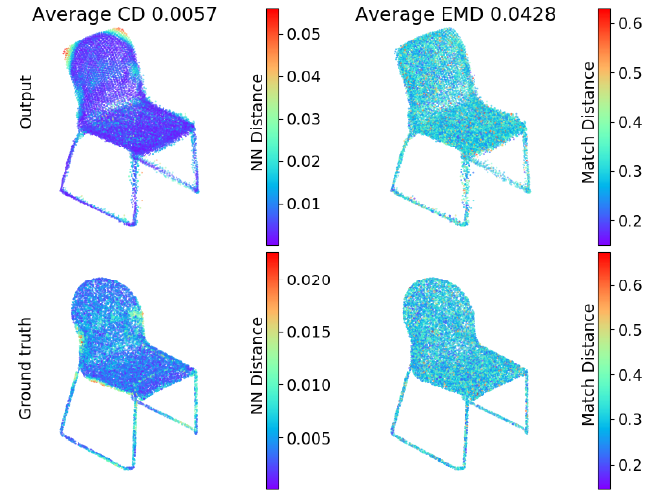
image-20211222141804355

图5：CD（左）和EMD（右）的插图表示。上面一行展示了我们的模型的输出，下面一行展示了基准的输出。左边的点通过它们到其他点云最近点的距离上色（近邻距离，Nearest Neighbor Distance，NN）。右边的点通过最优双射下对应点的距离上色（匹配距离）。平均CD是近邻距离的均值，平均EMD是匹配距离的均值。

我们在距离场中使用的度量是输出距离场和基准距离场之间的$L_1$距离，跟[^8]中一样。为了在不同的维度上拥有可以比较的数字，我们将误差从体素距离转换为模型的测度空间距离。

新颖对象的泛化性

如图3b所示，我们的方法在新颖类别的对象上优于所有的基线。更加重要的是，我们的模型的性能并没有受到显著地影响，甚至在可视化不相似的类别中（如：图9中的手枪）。这个说明通过我们的模型学习得到了形状先验。

体素方法的比较

可以看出，我们的方法无论在CD还是在EMD上都显著地优于3D-EPN方法。为了更好地解释数字，在图4a和图4b上，我们展示了对于测试集中的每个实例，我们的基于CD和EMD的补全结果相比3D-EPN都有巨大的提升。此外，它们还改善了3D-EPN上误差很大的例子，说明它们具有处理具有挑战性的、先前的方法处理失败的例子的能力。

在图4c中，我们的模型的输出被转换为距离场时获得了更低的$L_1$距离。而且，我们的方法相比3D-EPN在高分辨率上改进更加显著。

解码器的比较

在图3中，我们提出的解码器与现在的解码器设计进行了比较。我们设计的多步骤网络混合了全连接解码器和基于折叠的解码器的优点，并且获得了比它们更好的结果。依据定性的结果，我们发现全连接解码器在输出点的局部稠密上没有提供任何约束，并且输出点经常在区域中过度中心化（如：桌子的表面），这样会导致很高的EMD值。另一方面，基于折叠的解码器经常产生在空间中浮动的点，并且与基准数据的全局几何性质不一致，这样会导致很高的CD值。这是因为我们的数据集的形状包括许多凹面和尖锐的边，这使得全局折叠一个2D平面到一个3D形状非常具有挑战性。FoldingNet[^60]通过链接两个折叠操作来解决这个问题。然而，仅通过局部的折叠操作，我们的解码器仅使用一次折叠操作就能够获得更好的性能。

编码器比较

图3中的另一对比较是堆叠的PN和PN2[^38]分别作为编码器。PN2是层次特征提取网络的代表，这类网络在全局池化之前将局部信息聚集在一起。我们的结果说明堆叠PN的编码器效果更优，因为堆叠PN的编码器仅使用了全局池化。我们相信，对于我们处理的局部数据，由于局部近邻选择中的子优化，局部优化没有全局优化稳定。因此，我们认为使用堆叠PN层代替局部池化是混合局部信息和全局信息的更好的方法。

参数数量

表1：可以训练的模型参数的数量

方法 3D-EPN FC 折叠 PN2 PCN
参数数量 5240万 5320万 240万 679万 685万

如表1所示，我们的模型相比3D-EPN和FC在参数数量上少了一个数量级，同时明显地获得了更好的性能。

遮挡和噪声的稳健性

现在，我们的方法测试传感器噪声和大尺度遮挡的稳健性。具体来说，我们使用高斯噪声（标准差是深度图度量的0.01倍）扰动了深度图，并且用一个掩膜（覆盖$p%$个点）进行遮挡，$p$的取值为$0%$到$80%$。此外，我们随机设计$1%$的试题值为$d_{max}=1.6$。

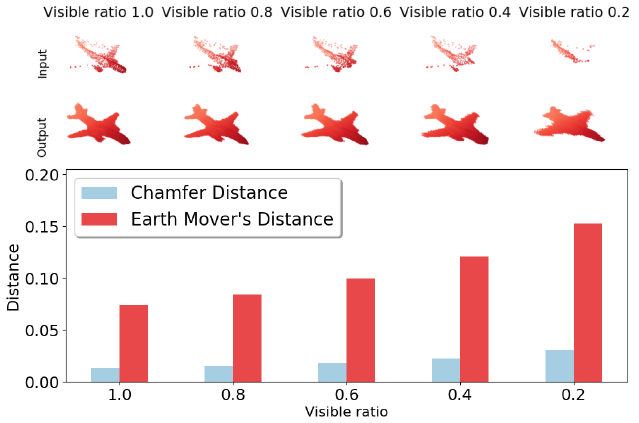
image-20211222151528124

图6：基于不同水平的可见性带噪声的输入产生的定性（上）与定量（下）的结果。

如图6所示，（CD和EMD）的误差是依据遮挡区域的大小逐步增长的。请注意，我们的模型没有基于这些遮挡和噪声样例进行训练，但是它们依然对其保持稳健性。模型学习得到的很强的形状先验帮助模型忽略噪声点，并且在遮挡下预测合理的输出。这个表现部分地说明了模型在真实世界的数据下也具有很强的泛化性，就如我们在后续的章节中展示的那样。

5.3. KITTI的补全结果

在本次实验中，我们的补全方法检测了从真实世界的激光雷达中扫描的局部点云数据。具体来说，我们从KITTI数据集中执行了一系列的Velodyne（激光雷达生产商）扫描[^13]。我们提取每一帧中标记为汽车的对象边界框内的点，从而产生2483个局部点云。每个点云都被转换为盒子的坐标，用一个从ShapeNet的汽车上训练的PCN进行补全，并且转换回世界坐标帧，操作过程参考图16。我们使用一个专门在汽车上训练的模型来整合对象类别的先验知识。拥有这样的先验知识对于我们的方法来说并非必要，但是可以帮助模型获得更好的性能。

image-20211223135141818

图16：KITTI的定性补全结果

我们没有KITTI的补全的基准点云数据。因此，我们提出了三个代替的测度去评估模型的性能：

  1. 保真度。这是输入的输入的每个点到输出中它的最近邻点的距离均值，这个测度表明输入的保留程度。
  2. 最小匹配距离（Minimal Matching Distance，MMD）。它是输出和ShapeNet的汽车点云之间的倒角距离（Chamfer Distance，CD），这个测度表明就CD而言，其最接近输出点云的程度。
  3. 一致性。这是连续帧中相同实例的补全输出之间的CD均值。这个测度表明网络的输入与输出之间的变化程度。作为比较，我们还计算了连续帧的输入之间的CD均值，表示为一致性（输入）。这些指标在表2中报告。

表2：KITTI的定理结果

保真度 MMD 一致性 一致性（输入）
0.02800 0.01850 0.01163 0.05121

与来自2.5D图像反向投影成点云不同，来自激光雷达扫描的点云非常稀疏。2483个局部点云平均包含440个点，某些点云中点的数量甚至低于10个。相反，训练中使用的来自2.5D图像的点云中点的数量经常超过1000个。尽管如此，我们的模型能够在无需什么精调的情况下，在两个分布之间轻松地转换，从极端的局部输入中生成一致的补全。这个结果可以归因于使用了基于点的表示方法，相比体素表示方法其敏感性更低。此外，我们的模型的每次预测在Nvidia GeForce 1080Ti GPU上只需要0.0012秒，在3.6GHz Intel Core i7-7700 CPU 上只需要2秒，证明它非常适合实时应用。

5.4. 基于补全实现点云配准

点云上的许多常见任务都可以受益于更加完整和稠密的输入。在这里，作为这种应用的例子，展示了我们的网络可以改善点云配准的结果。具体来说，我们对来自Sec0503的相同的Velodyne序列中的相邻帧的汽车点云执行配准，使用PCL[^40]中实现的简单的点对点ICP[^5]算法。这样产生了2396个配准实例。我们向配准算法提供了两种输入：一种来自原始扫描的局部点云；一种是从ShapeNet的汽车类别上训练的PCN生成的补全点云。我们比较了局部输入和全局输入中配准结果上的旋转误差和平移误差。旋转误差的计算公式：$2\cos^{-1}(2\langle q_1,q_2\rangle^2-1)$，其中$q_1,q_2$是基准旋转的四元数表示，并且旋转计算来自ICP。这个结果度量了$q_1,q_2$之间的角度。平移误差的计算公式：$|t_1-t_2|_2$，其中$t_1$是基准平移，$t_2$是通过ICP计算的平移。

如图7a和图7b中所示，由PCN产生的补全点云，旋转和平移估计更加精确，并且显著地改善了局部点云的较大误差。图7c展示了一些定性的例子。可以看出，完整的点云更容易配准，因为它们包含了更大的重叠，那么重叠的区域中很大一部分是PCN补全的。请注意，我们的补全结果带来的改善不仅针对于ICP，还可以应用到任意的配准算法中。

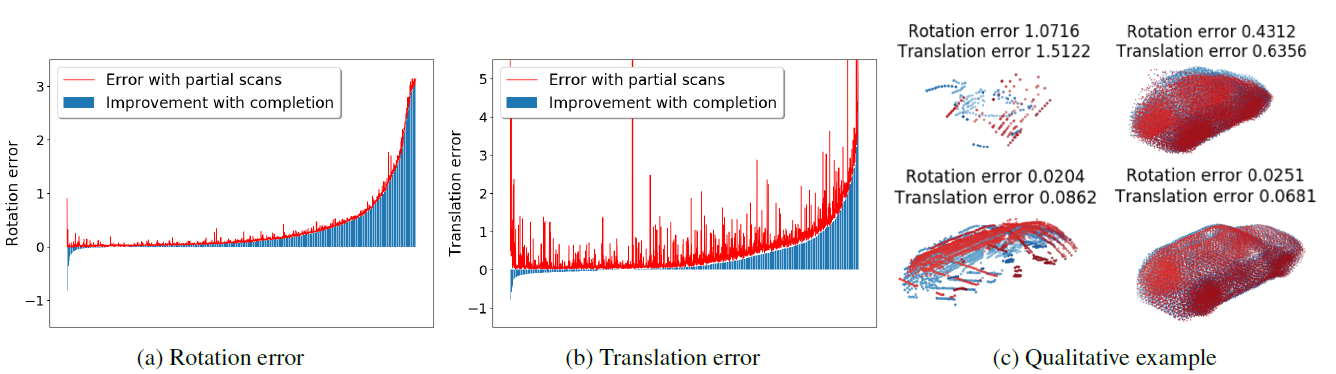
image-20211222165511602

图7：点云配准的改进。在(a)和(b)中，x-轴表示不同的配准实例。蓝色竖条的高度表示相比局部点云配准，补全点云配准的改进程度。红色曲线是局部点云的配准误差。红色曲线和蓝色竖条之间的差是补全点云的配准误差。在(c)中，同样的实例配准后的局部点云（左）和配准后的补全点云（右）

Ch06 讨论

根据我们的模型，已经可以确定两个主要的错误模式：

  1. 有些对象实例由多个断开的部件组成。我们的模型没有意识到这一点，并且错误地将部件连接到一起。这很可能是从训练数据集中学到的强先验导致的结果，因为数据集中的对象几乎都是连接在一起的 。
  2. 有些对象包含非常细薄的结构，例如：电线。我们的模型有的时候不能恢复这样的结构。这存在两种可能：
    1. 来自这些结构的点通常是稀疏的，因为它们的表面积很小使得3D特征抽取更加困难
    2. 与大多数对象的表面不同，细薄结构的局部几何性质与2D栅格没有相似性，这使得我们的模型很难将2D栅格变形为这类细薄结构。

这些失败案例的部分可视化参见图8。

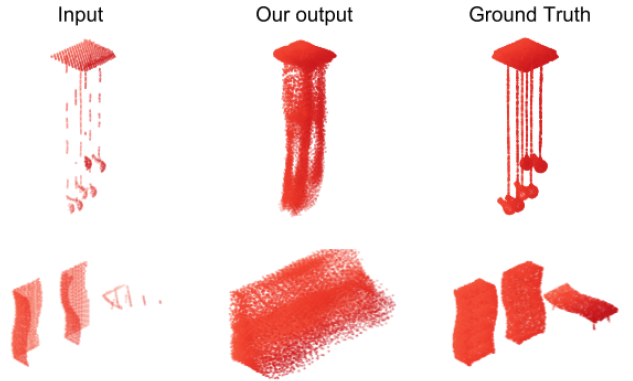
image-20211222165347319

图8：失败模式：细薄结构（上）和断开组件（下）

Ch07 结论

我们已经提出了一种使用点云而无需体素化执行形状补全的新方法。为此，我们设计了一个深度学习架构，结合了现存结构的优点使用一种从粗到细的方式去生成稠密点云，相比基于体素的模型使用更少的参数实现高分辨率补全。我们的方法对于多种对象类别都有效。此外，模型对于未见过的对象和真实世界的数据表现了很强的泛化性能。我们的基于点的补全方法相比基于体素的方法更具扩展性和稳健性，这使得它更适合处理更加复杂的数据（如：场景数据）。

附录

A. 概论

在本文的主体中，我们提供了技术细节和附加的定量与定性结果。接下来：

B. 局部折叠操作

在这里，我们详细描述了Sec0402中提及的局部折叠操作。如图10所示，折叠操作在粗略输出$Y_{coarse}$和$k$维全局特征$\mathbf{v}$中取点$\mathbf{q}_i$作为输入，并且在以$\mathbf{q}_i$为中心的局部坐标中通过变形$u\times u$栅格生成$t=u^2$个点的块。它首先在以零点为中心的边长为$r$（$r$控制输出块的尺寸）的$u\times u$大小的栅格中取点，然后组织它们的坐标为$t\times2$的矩阵$G$。然后，它使用中心点$\mathbf{q}_i$和全局特征向量$\mathbf{v}$的坐标拼接$G$的每一行，并且通过共享的MLP传递结果矩阵生成$t\times3$的矩阵$Q$，即以$\mathbf{q}_i$为中心的局部块。这个共享MLP可以被解释为一个非线性变换，用于将2D栅格变换为3D空间中的平滑的2D流形。注意到相同的MLP被用于为每个$\mathbf{q}_i$的局部块生成中，因此参数的数目在局部折叠操作不会增长得超过输出的大小。

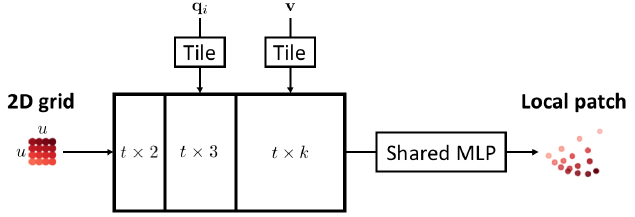
image-20211223100412008

图10：折叠操作

C. 网络架构细节

在这里，我们介绍了相比Sec0502的模型架构的细节。我们使用的3D-EPN模型是3D-EPN-UNet-class，来自于[^9]的最佳效果模型。对于见过的类别，我们使用$128^3$输出，其中包含了附加数据集的检索步骤。对于未见过的类别，我们使用原始的来自于模型的$32^3$的输出。

堆叠的PN编码器用在了全连接网络（FC）、折叠网络（Folding）、PCN-CN 和 PCN-EMD（包含2个PN层）中。共享MLP在第一个PN层拥有2个层（128，256）。共享MLP在第二个PN层拥有两个层（512，1024）。我们模型拥有的PN2编码器与SSG网络[^38]中是相同的架构。

D. ShapeNet的其他结果

表3：关键点数目对比输入点数目

点的平均数
输入 1105
关键点（第一个PN层） 101
关键点（第二个PN层） 363

表4：ShapeNet数据集中已知类别的倒角距离（CD）

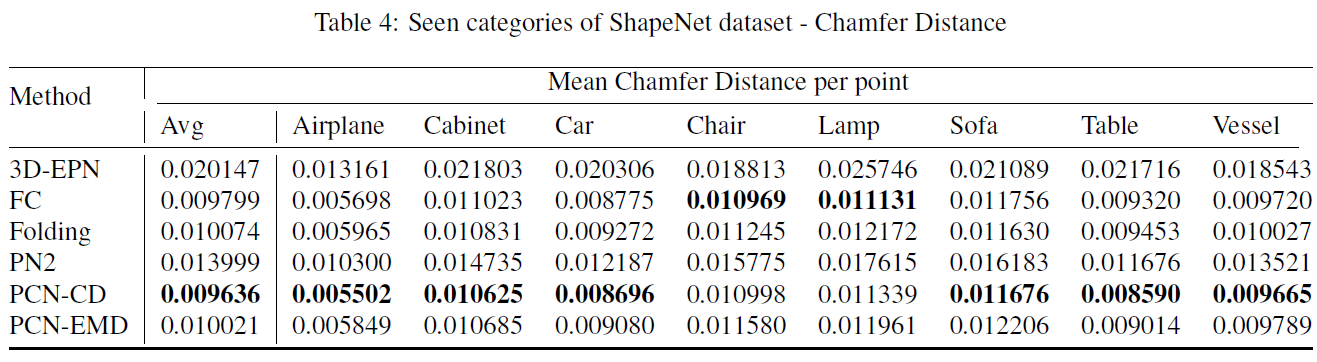
image-20211223104414341

表5：ShapeNet数据集中已知类别的地动距离（EMD）

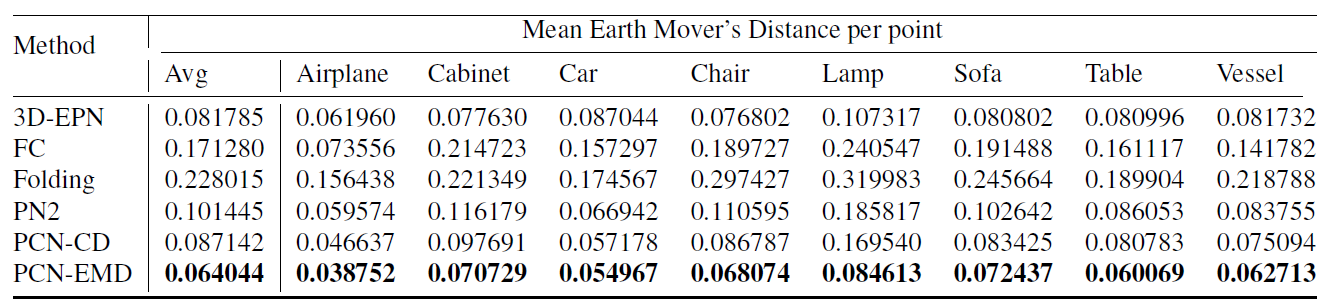
image-20211223104520877

表6：ShapeNet数据集中未知类别的倒角距离（CD）

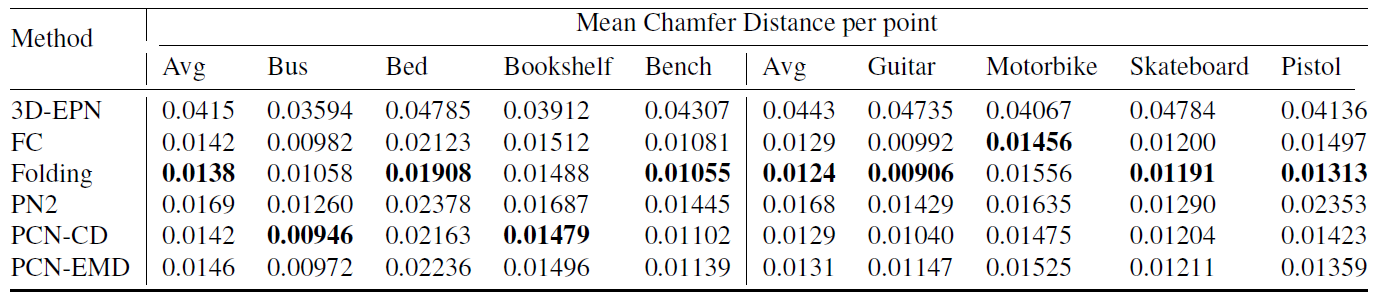
image-20211223104607521

表7：ShapeNet数据集中未知类别的地动距离（EMD）

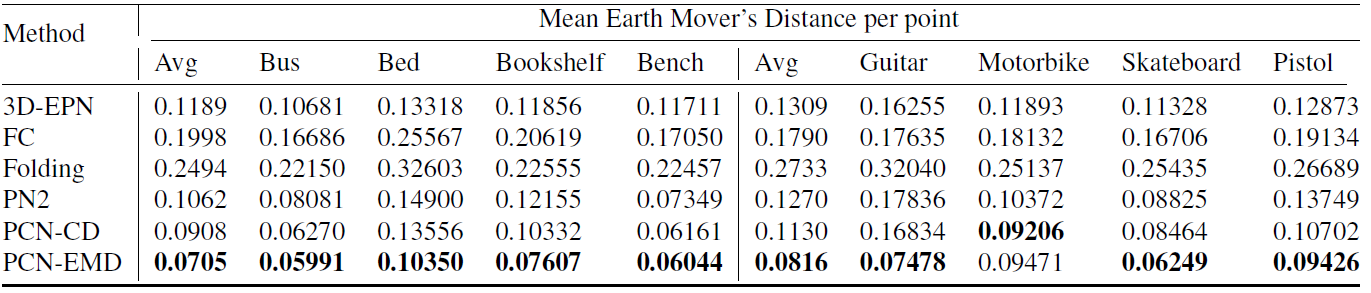
image-20211223104735712

表4，5，6和7显示了来自ShapeNet的测试实例的定量结果，与论文主体中的表 3形成了对比。图9展示了来自于已知类别和未知类别的形状的定性比较。如我们所见，3D-EPN的输出经常包含缺失的或者多余的部件；FC的输出是精确的，但是点过于集中在某些区域；Folding的输出包含了许多浮动的点；PN2的输出是模糊的；我们的模型的输出在全局几何性质和局部点密度上与基准数据匹配地最好。

E. KITTI的其他结果

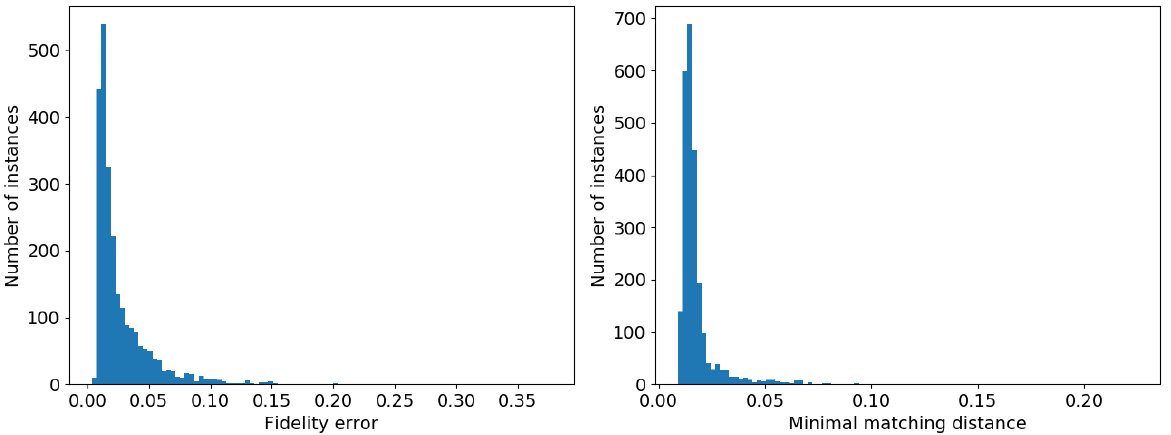
image-20211223104830006

图11：在KITTI汽车补全中保真度误差和最小匹配距离的分布

image-20211223105107969

图12：KITTI的汽车模型（左）、补全模型（中）和匹配模型（右）。右边的匹配模型是来自ShapeNet中的基于倒角距离最接近补全输出的汽车点云。图（上）展示了成功的补全，图（下）展示了由于错误的分割导致的失败案例。

图11显示了在KITTI的补全结果上保真度误差和最小匹配距离的分布。可以看出存在少量的错误案例拥有非常高的误差导致Sec0503中报告的均值发生偏差。图12展示了一些定性的案例。我们基于大量的这种案例观测可知，我们的模型生成了一个有效的汽车形状，同时这个形状与ShapeNet中匹配的模型不同，结果如图12（上）所示。然而，我们还观察到某些失败的案例，如：图12（下）由地面上的额外点或者汽车边界框内的附近物体引起的。这个问题可以通过在传递局部点云到PCN之前增加一个分割步骤给予隐性地解决。

F. 更多的架构分析

堆叠PN层的效果

在这里，我们测试了在编码器中拥有不同数目的堆叠PN层的PCN-CD。图13展示了ShapeNet测试集的均值CD和EMD。显而易见，使用2个堆叠PN层好过使用1个的，使用多个堆叠PN层的好处是微乎其微。这里说明2个堆叠PN层在输入中充分地混合了局部的和全局的几何信息。因此，我们在实验中使用2个堆叠PN层，即使使用更多的PN层能够进一步改善PCN的性能。

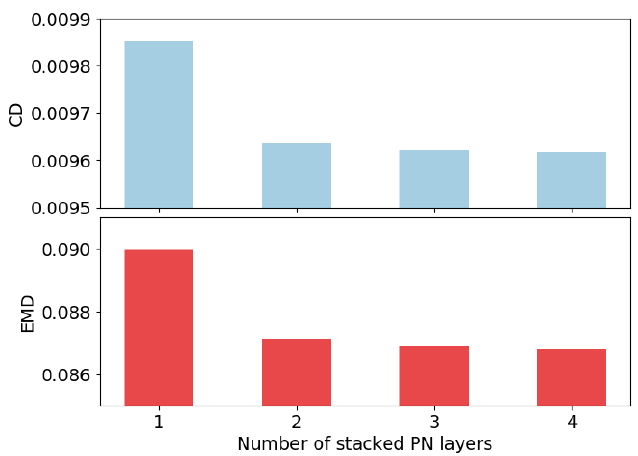
image-20211223110406361

图13：PN层的不同数目的测试错误

瓶颈大小的影响

在这里，我们测试了不同瓶颈大小的PCN-EMD，即全局特征向量$\mathbf{v}$的长度。ShapeNet测试集上的CD的和EMD的均值如图14所示。可以看出PCN的性能随着瓶颈尺寸变大而变好。在我们的实验中，我们选择瓶颈尺寸为1024，因为更大的瓶颈尺寸2048的模型无法装入到单个GPU内存中。这个意味着使用多个GPU进行训练，PCN的的性能会随着瓶颈尺寸变大而变好。

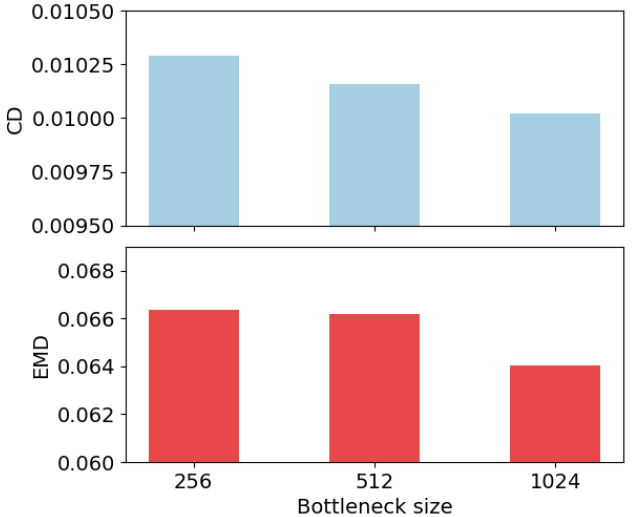
image-20211223110452713

图14：不同的瓶颈大小的测试错误

G.更多的可视化

关键点可视化

如[^37]中所述，PN层可以被解释为用于描述形状所选择的关键点的集合。更具体地说，共享MLP的每个输出单元都可以被看作点云的函数。点云中选择的关键点是达到了这些点函数中至少一个达到了最大值的点。换句话说，它们是其特征值被最大池化操作“选择”到最终特征向量中的点。请注意，通过实现多个特征函数的最大值，可以多次选择相同的点。事实上，如表3所示，通常情况下，关键点的数量远小于瓶颈大小（1024）或者输入点的数量。这意味着只要这些关键点被保留下来，那么所学到的特征就不会改变。这个性质保证了我们的模型对噪声的稳健性。

在图15中，我们将堆叠PN编码器中的两个PN层选择的关键点进行了可视化。观察得到，两个PN层以从粗到细的方式总结了形状：

image-20211223114005051

图15：关键点可视化

请注意，这种从粗到细的描述是在没有任何显式地有监督的情况下出现的。

特征空间可视化

在图17中，我们使用t-SNE[^27]将ShapeNet测试案例中的1024维的全局特征嵌入表示到2D空间中。可以看出形状通过它们的语义分类聚集在一起。请注意，这个依然是没有任何有监督的情况下发生的行为，因为我们没有在全部训练期间使用分类标签。

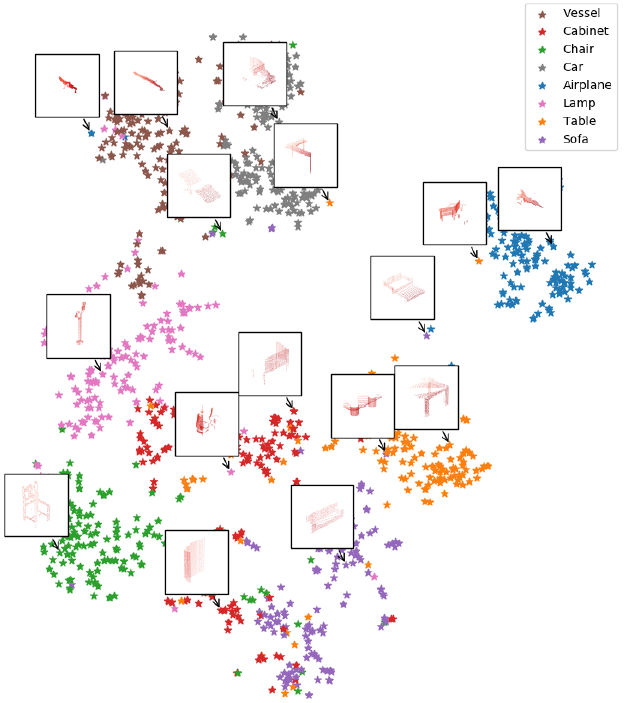
image-20211223135334521

图17：在局部点云上学习得到的特征的T-SNE嵌入表示

深度学习（花书）第八章
Fundamentals_of_ComputerGraphics_PeterShirley